This specification contains all details of Sphinx packet data structures and algorithms for constructing/unwrapping Sphinx packets.

Please note that this specification is exactly the same as what defined in the Sphinx paper below and what implemented by Nym: https://github.com/nymtech/sphinx.

Therefore, this document covers only an overview of Sphinx packet construction with easy-to-understand diagrams. For more details, please see the executable specification written in Python.

Sphinx Packet Construction

Header Construction

A diagram below describes how a Sphinx header is constructed.

  • A Sphinx header contains encapsulated routing information.
  • Given a mix route with three mix nodes $m_1, m_2, m_3$, and a mix destination $m_D$, a routing information of each $m_2, m_3, m_D$ is encapsulated in a Sphinx packet as below.
    • A routing information of $m_1$ is not encapsulated in the packet because a packet sender, who chooses a mix route, always know the information of $m_1$.

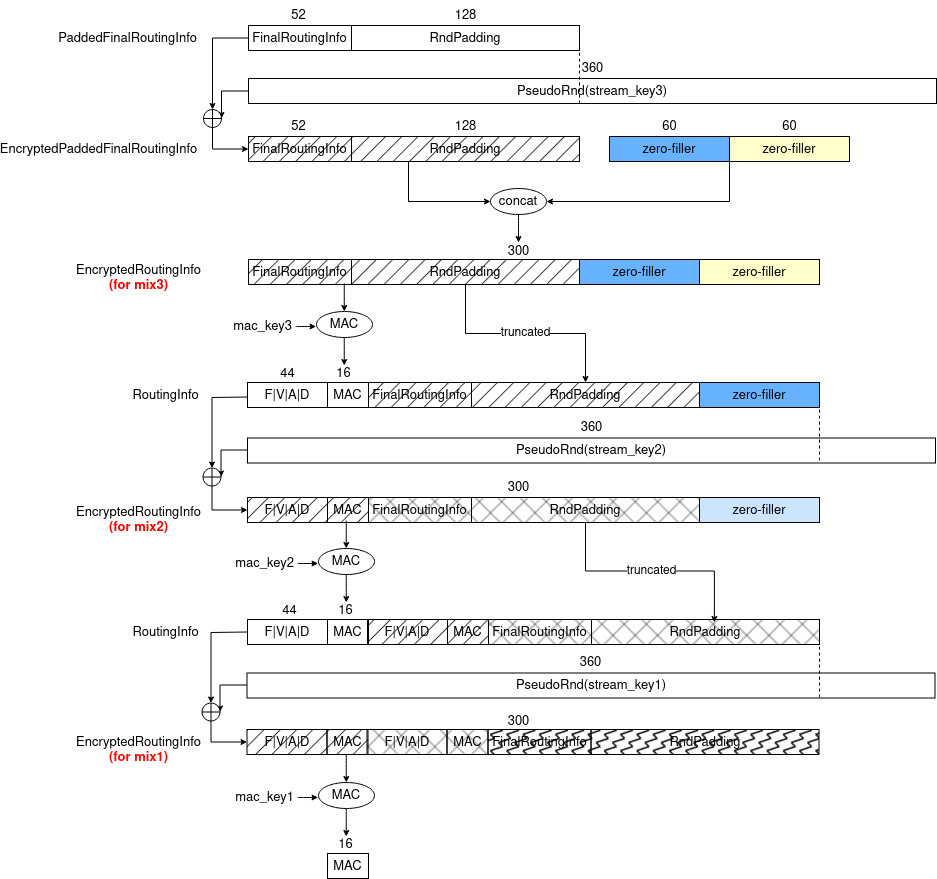
Routing Information Encryption

  • A routing information (RoutingInfo or PaddedFinalRoutingInfo) is encrypted by XOR operation with a pseudo-random bytes generated by AES128-CTR using a private key of $m_l$ and a constant nonce.
  • The reason why XOR is used separated with AES128-CTR is making zero fillers can be re-appended seamlessly as if they have not been truncated.

Routing Information Filler Construction

In the Header Construction diagram, two zero fillers (encrypted; colored) are appended to the EncryptedPaddedFinalRoutingInfo to make it have the same size as EncryptedRoutingInfo (300 bytes).

Also, when constructing a RoutingInfo of $m_3$, the last filler is truncated. And, the remaining filler in the RoutingInfo is encrypted again with a stream key of $m_2$ to build a new EncryptedRoutingInfo (300 bytes).

That is, the filler is for preventing adversaries from distinguishing packets emitted from different mix layers (i.e. packet-layer undistinguishability).

The diagram below shows how fillers can be constructed and encrypted. The zero-filler is a 60-byte x00 byte array.

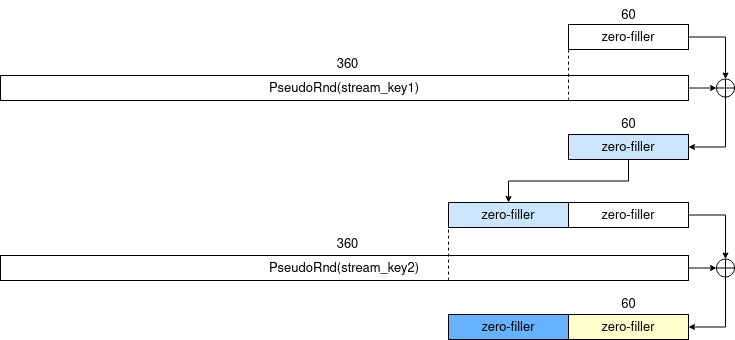
Because an additional XOR is used separately with AES128-CTR for encryption, the truncated filler can be easily recovered when a mix node decrypts a EncryptedRoutingInfo. For example,

  • $m_1$ appends a zero filler to the EncryptedRoutingInfo, and decrypts it using XOR with the same pseudo-random bytes that was used when the EncryptedRoutingInfo was created.
  • This XOR converts the zero filler appended to an encrypted-once filler (the sky-blue filler in the diagram) because of the characteristics of XOR and the position of the pseudo-random bytes that is XOR-ed.
  • In the same manner, $m_2$ can also recover the blue filler and the yellow filler, which can be forwarded to the $m_3$ finally.

The more detailed explanation can be found below:

  • RND: $A_{60}B_{60}C_{60}D_{60}E_{60}F_{60} \leftarrow \text{PRNG}(key)$

    \[\text{PRNG}(key) = \text{AES128CTR}(key, iv_{const}, 0_{60}0_{60}0_{60}0_{60}0_{60}0_{60})\]
  • Filler (60*2 bytes): $(F \oplus E)F$
  • encrypted by $m_1$: $XXX$
    • and, $m_1$ adds the filler: $XXX \rightarrow XXX(F \oplus E)F$
  • encrypted by $m_2$: $YX’X’X’(F \oplus E \oplus E)=YX’X’X’F$

  • encrypted by $m_3$: $ZY’X’X’X’$

  • $m_1$ decrypts: $ZY’X’X’X’0 \rightarrow M_2YXXXF$
    • So, $YXXXF$ is passed to $m_2$ because $m_1$ truncates $M_2$ that is the $m_2$ info.
  • $m_2$ decrypts: $YXXXF0 \rightarrow M_3XXX(F \oplus E)F$
    • So, $XXX(F \oplus E)F$ is passed to $m_3$ because $m_2$ truncates $M_3$ that is the $m_3$ info.
  • $m_3$ removes the filler: $XXX(F \oplus E)F \rightarrow XXX$
    • and decrypts $XXX$

Payload Construction

Payload construction is simpler than the header construction.

A payload is leading/trailing padded as below:

padded_payload = zero_bytes(16) + payload + b"\x01" + zero_bytes(T)

The T is determined to make the size of padded_payload 1024 bytes.

If payload is too large to make padded_payload 1024 bytes, the algorithm fails.

The padded_payload is layered-encrypted by Lioness with ChaCha20 and Blake2b using a payload key of each $m_1, m_2$ and $m_3$.